Sabtu, 26 Februari 2011

GELOMBANG MEKANIK
A.
Gelombang Berjalan
Gelombang Mekanik adalah perambatan energi yang melalui suatu medium, untuk gelombang berjalan berlaku
persamaan:
(
)
kx
t
A
y
m
ω
sin
±
=
DenganA = amplitudo,ω= frekwensi sudut dank = bilangan gelombang (2π/λ),t = waktu getar dan cepat
rambat gelombang berjalan adalah:
t
vλ
=
B.
Kecepatan Getar Partikel
Kecepatan partikel naik-turun di suatu titik pengamatan (P) adalah:
(
)
kx
t
A
vp
−
=
ω
ωcos
C.
Percepatan Getar Partikel
Percepatan partikel naik-turun di suatu titik pengamatan (P) adalah:
(
)
y
kx
t
A
ap
2
2sin
ω
ω
ω
−
=
−
−
=
D.
Sudut Fase Gelombang
p
p
x
Tt
kx
t
πϕ
λ
π
ω
θ
2
2
=
−
=
−
=
denganϕp = fase gelombang di titik pengamatan.
π
θ
λ
ϕ
2
p
p
x
Tt
=
−
=
Beda fase antara titik A dan B adalah
(
)
A
B
A
B
x
x
x
x
x
x
−
=
∆
−
−
=
∆
−
=
∆
;
λ
λ
ϕ
Tanda negatif menunjukkan bahwa partikel di depan mengalami keterlambatan fase terhadap partikel di
belakangnya.
E.
Gelombang Stasioner
Gelombang stasioner terjadi karena interferensi terus menerus antara gelombang datang dan gelombang pantul.
Gelombang stasioner dengan ujung tetap
kx
A
A
t
A
t
kx
A
y
s
s
sin
2
;
cos
cos
sin
2
=
=
=
ω
ω
Letak simpul
4
2
1
λ
×
=
+
n
xn
Letak perut
(
)4
1
2
1
λ
+
=
+
n
xn
Gelombang stasioner dengan ujung bebas
kx
A
A
t
A
t
kx
A
y
s
s
cos
2
;
sin
sin
cos
2
=
=
=
ω
ω
Letak simpul
(
)4
1
2
1
λ
+
=
+
n
xn
Letak perut
4
2
1
λ
×
=
+
n
xn
DenganA = Amplitudo gelombang berjalan,As = Amplitudo gelombang tetap, n = 0, 1, 2, …
F.
Cepat Rambat Gelombang Trasversal Dalam Dawai
A
L
m
A
F
F
v
ρ
µ
ρ
µ
=
=
=
=
;
dengan:ρ = massa jenis dawai, A = luas penampang dawai,µ = massa dawai per satuan panjang daw.

Getaran bebas tanpa peredam


Model massa-pegas sederhanal
Pada model yang paling sederhana redaman dianggap dapat diabaikan, dan tidak ada gaya luar yang mempengaruhi massa (getaran bebas).
Dalam keadaan ini gaya yang berlaku pada pegas Fsx, sesuai dengan hukum Hooke, atau bila dirumuskan secara matematis: sebanding dengan panjang peregangan
F_s=- k x \!
dengan k adalah tetapan pegas.
Sesuai Hukum kedua Newtonpercepatan gaya yang ditimbulkan sebanding dengan massa:
\Sigma\ F = ma = m \ddot{x} = m \frac{d^2x}{dt^2} =
Karena F = Fs, kita mendapatkan persamaan diferensial biasa berikut:
m \ddot{x} + k x = 0.

Gerakan harmonik sederhana sistem benda-pegas
Bila kita menganggap bahwa kita memulai getaran sistem dengan meregangkan pegas sejauh A kemudian melepaskannya, solusi persamaan di atas yang memerikan gerakan massa adalah:
x(t) = A \cos (2 \pi f_n t) \!
Solusi ini menyatakan bahwa massa akan berosilasi dalam gerak harmonis sederhanaamplitudo Afn. Bilangan fn adalah salah satu besaran yang terpenting dalam analisis getaran, dan dinamakan frekuensi alami takredam. Untuk sistem massa-pegas sederhana,ndidefinisikan sebagai: yang memiliki dan frekuensi f
f_n = {1\over {2 \pi}} \sqrt{k \over m} \!
Catatan: frekuensi sudut ω (ω = 2πf) dengan satuan radian per detik kerap kali digunakan dalam persamaan karena menyederhanakan persamaan, namun besaran ini biasanya diubah ke dalam frekuensi "standar" (satuan Hz) ketika menyatakan frekuensi sistem.
Bila massa dan kekakuan (tetapan k) diketahui frekuensi getaran sistem akan dapat ditentukan menggunakan rumus di atas.

[sunting] Getaran bebas dengan redaman

Mass Spring Damper Model
Bila peredaman diperhitungkan, berarti gaya peredam juga berlaku pada massa selain gaya yang disebabkan oleh peregangan pegas. Bila bergerak dalam fluidac ini dinamakan koefisien peredam, dengan satuan N s/m (SI) benda akan mendapatkan peredaman karena kekentalan fluida. Gaya akibat kekentalan ini sebanding dengan kecepatan benda. Konstanta akibat kekentalan (viskositas)


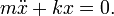
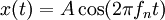
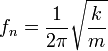
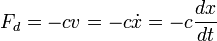
F_d = - c v = - c \dot{x} = - c \frac{dx}{dt} \!
Dengan menjumlahkan semua gaya yang berlaku pada benda kita mendapatkan persamaan.








 
Diposting oleh di
Label:

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)